发布时间:2022-05-21
2022年5月20日上午,山西大学120周年校庆“科技史系列讲座”第14期开讲,我所邀请到电子科技大学万小龙教授作了题为《作为量子信息基础的模态逻辑四个等价性——兼论科技思想史的启发》的学术报告。万小龙教授是电子科技大学“科技的哲学、逻辑与历史”研究中心主任,国家马克思主义工程“科学技术哲学”首席专家之一。本次报告通过“腾讯会议”线上平台举行,由我所乔笑斐副教授主持。

讲座伊始,万教授向山西大学120周年校庆表示了祝贺,随后围绕主题从四个部分展开报告:
第一部分是关于模态逻辑的基础介绍。STRF理论(函数狭义相对论)是万教授的原创探索性理论,万教授举了多个生动形象的例子,系统性地介绍了STRF理论的前提、出发点、基础语义和研究进展。万教授指出,虽然克里普克的可能世界语义学等研究获得了巨大成功,但在数学角度和形而上学角度仍存在许多难题。在历经多年的探索与研究后,万教授从质疑冯·诺依曼量子逻辑非分配性和“四个基础”出发,于2014年草创STRF理论时提出了第一个等价性,再给量子信息基础以简要解释,提出作为量子信息基础的模态逻辑的四个等价性,即真值函数系统SF与非真值函数系统SFE的严格等价、非真值函数式簇对于必然算符等价、一元实体赋值与二元背景赋值等价、去冗的标准语义等价。
第二部分是关于模态逻辑的真值函数系统SF与非真值函数系统SFE的严格等价的阐述。万教授给出了严格隐变量定义:任意等价形式A与B,如A有变量x而B无,则x为B相对于A的隐变量。严格隐变量能够增加对非经典逻辑的解释与表达力,在量子力学中,标准形式下增加量子式或变量将形成超量子力学。以广义形式的薛定谔方程为例,![]() 中的虚数单位i、表征波函数总能量的哈密顿算符
中的虚数单位i、表征波函数总能量的哈密顿算符![]() 和物理系统的波函数
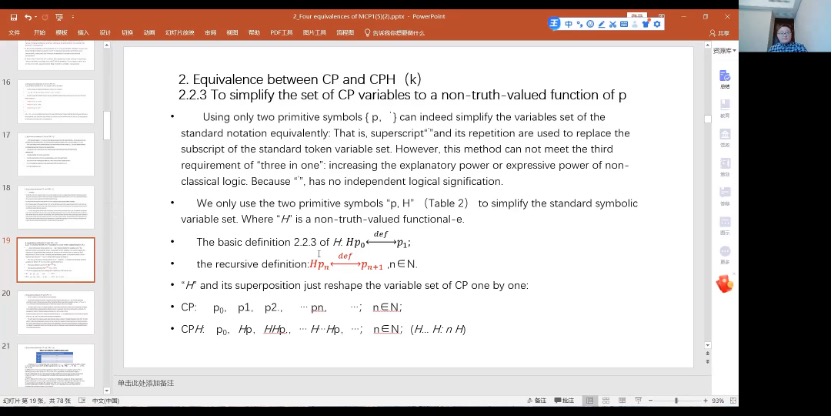
和物理系统的波函数![]() 之中也必然存在严格隐变量。2019年,寻找非经典逻辑的句法或语义严格隐变量已经成功。万教授还引入了平凡严格隐变量,又称平庸严格隐变量,即仅能做到简化与等价、而不能够增加对非经典逻辑的解释和表达力的隐变量。随后,万教授介绍了CPH记号体系,其由CP标准记号体系严格等价简化,仅用“p,H”两个符号就可等价简化标准记号变元集,经等值变换可导致非真值函数式下标与其直接联结的公式保持一致。在此体系下,
之中也必然存在严格隐变量。2019年,寻找非经典逻辑的句法或语义严格隐变量已经成功。万教授还引入了平凡严格隐变量,又称平庸严格隐变量,即仅能做到简化与等价、而不能够增加对非经典逻辑的解释和表达力的隐变量。随后,万教授介绍了CPH记号体系,其由CP标准记号体系严格等价简化,仅用“p,H”两个符号就可等价简化标准记号变元集,经等值变换可导致非真值函数式下标与其直接联结的公式保持一致。在此体系下,![]() ,隐藏上下标体现极致简单与严密性,揭示“伪”等值代换不成立有重要意义。
,隐藏上下标体现极致简单与严密性,揭示“伪”等值代换不成立有重要意义。
第三部分是关于非真值函数式簇对于必然算符等价的介绍。万教授从“簇”的定义出发,将CPH增加一个辅助性符号“■”,以提供揭示模态本性的助发现法。“■”的直接意义是作为CPH中一簇家族类似的非真值函数式的方便记号,簇记号法叫“黑模法”(BCP),包含“■”的公理简称黑模。万教授指出,BCP中能够使得包含■的公理称为经典定理的非真值函数式的簇,BCP对CPH中非真值函数也是对CP中真值函数进行分类研究。在同时出现■A和■B时,隐藏的上标对应簇展开为公式系列:■A对应(A,A0),(A,A1)…(A,An),■B对应(B,B0),(B,B1)…(B,Bn)。簇“■”是一般性非真值函数联结词,具有强大统一的逻辑(智能)表达功能。
第四部分是关于标准语义的去冗等价的解读。万教授讲述了一元实体赋值与二元背景赋值等价的引入、核心簇语义的定义、核心簇语义与其他两种典型语义(莱布尼兹、克里普克)的比较及相关问题的解释。万教授指出,簇语义可表示事物与其生存环境(背景世界)的相互依赖,而标准语义只表示事物对其环境的依赖,极少用之表达整体性和辩证性。万教授还介绍了叠置算符问题、对公理的模型有效性影响、必然化规则的再认识等内容,得出了去冗的标准语义即簇语义的结论,即MCP是具有簇子结构的CP,“可能世界”是CP中作为赋值语境的命题,MCP公理是对CP命题的分类研究,去冗标准语义就是簇语义。万教授还以人工智能为例,解释了其目前面临的表达整体辩证及不确定性难题。
整场讲座,万教授引经据典、旁征博引,向各位师生介绍了STRF理论的一系列原创性成果。万教授通过真性模态命题逻辑(MPC)的研究,证明了在量子计算和量子信息中,MPC与经典命题逻辑(CP)的等价性。在提问与讨论环节,武汉大学桂起权教授对万教授的研究给予了高度评价,与会师生针对报告内容进行了热烈的讨论与交流。
通讯撰稿 | 路昊明
通讯审稿 | 袁紫玉
网页编辑 | 王 坚
